Try the following GMAT Problem Solving question that tests your ability to find areas of intersections of circles.
Question 41:
Three semicircles of radius 1 are constructed on diameter ¯AB of a semicircle of radius 2. The centers of the small semicircles divide ¯AB into four line segments of equal length, as shown below. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?
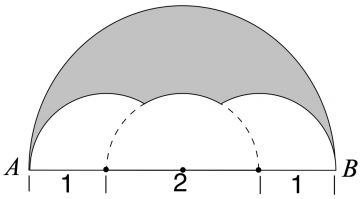
-
π−√3
-
π−√2
-
π+√22
-
π+√32
-
76π–√32
Leave a Reply