I just published my video explanations to all of the 84 quantitative reasoning questions that I encountered in my total of four attempts at GMAT Exams 5 and 6: 2024 GMAT Official Practice Exams 5 and 6 video explanations.

The GMAT Official Practice Exams 3 and 4 are excellent for test takers preparing for the GMAT exam. Each test can be reset twice, allowing students a total of four attempts. The tests are available for purchase from GMAC’s website and cost $60. Here are my observations after my four attempts at taking these two tests.

1. There were no repeats in any of the quantitative reasoning and data insight questions in all four exams. I did not check the verbal section, but I am assuming that would be the case there as well. GMAC does mention on their product description that each test can be reset twice, and this is indeed true. This means one can have a total of four practice test attempts from just the GMAT Exam 3 and 4. This was also the case with GMAT Exam 1 and 2(free ones), and will likely be the case with GMAT Exam 5 and 6(I have yet to confirm this 100%). What this means is that a student preparing for the GMAT has a total of 12 practice test attempts. This is a lot of practice tests, and should be sufficient for the large majority of students.

2. A lot of students try to save these exams for the end, but I would advise against that. These tests give you an excellent opportunity to learn the real experience of taking the GMAT. The GMAT test is fairly stressful and almost all test takers are at the edge of their ability, mainly because of the adaptive nature of the test. I urge all GMAT test takers to start taking full length practice tests early on and keep taking these throughout their preparation process. Yes, the GMAT Exam tests are expensive, but these are the closest to the real exam, and I urge all test takers to solely stick with these practice tests. Your time is far more valuable to spend it on free online tests of questionable quality.

3. One key strategy that I used in dealing with very difficult questions in quantitative reasoning section was to select an answer and flag that particular question and come back to it towards the end of the test. Because the new adaptive test gives this option, this approach can help to not get sucked into difficult questions and end up say spending six minutes on just question. You would be surprised how common that is during the testing process.

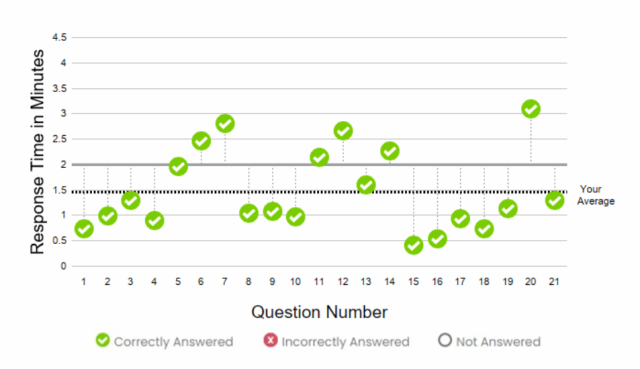
4. I also noticed that the average difficulty of the questions in my fourth attempt was significantly lower than the first three attempts(see attached image). I had almost 14 minutes left, which was not the case with the previous three attempts where I had roughly 5 minutes or less left. This is likely because of the smaller size of the question database in GMAT Exam 3 and 4. This will likely not be the case in the real official GMAT exam where the size of the question pool should be significantly larger.

I have also published my video explanations to all of the 84 quantitative reasoning questions and 24 data sufficiency questions organized on this page: 2024 GMAT Official Practice Exams 3 and 4 video explanations.