Algebraic expressions: GRE Quantitative Comparison Question#1
This GRE quantitative comparison question tests your understanding of being able to manipulate algebraic expressions.
$\begin{array}{c c c c c c c}
& & & a – 3b=\dfrac{9}{a+3b} & & & & \\
& & & \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & a^2 – 9b^2 & & & & 3 \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Quadratic equations: GRE Quantitative Comparison Question#2
This GRE quantitative comparison question tests your understanding of quadratic equations.
$$
\begin{array}{c}
x \gt 0 \\
(6x)^2 \, – (6x) \,- 12 = 0
\end{array}
$$
$\begin{array}{c c c c c c c}
& & & \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & x & & & & \dfrac{3}{4} \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Percent increase: GRE Math Practice Question#3
The price of an item in year 2000 was $p$ dollars. Each year after that the price was $10$ percent greater than the price for the previous year. What was the total percent increase in the price of the item from year 2000 to the year 2003?
- $\quad 30\%$
- $\quad 31.3\%$
- $\quad 32\%$
- $\quad 33.1\%$
- $\quad 36.3\%$
Mixtures and solutions: GRE Math Practice Question#4
How many liters of a $12$ percent alcohol solution must be added to $6$ liters of a $24$ percent alcohol solution to obtain a solution that is $15$ percent alcohol?
- $\quad 9$
- $\quad 15$
- $\quad 18$
- $\quad 20$
- $\quad 24$
Equation of straight lines: GRE Math Practice Question#5
In the $xy$-plane line $l$ has a slope of $m$ and a $y$-intercept of $b$, what is the $x$-intercept of the line $l$ in terms of $m$ and $b$?
- $\quad -\dfrac{b}{m}$
- $\quad -\dfrac{m}{b}$
- $\quad \dfrac{1}{bm}$
- $\quad \dfrac{b}{m}$
- $\quad \dfrac{m}{b}$
Triple Venn diagrams: GRE Math Practice Question#6
Of $28$ students taking at least one subject, the number taking Mathematics and English only equals the number taking Mathematics only. No student takes English only or History only, and six students take Mathematics and History, but no English. The number taking English and History only is five times the number taking all three subjects. If the number taking all three subjects is even and non-zero, the number taking English and Mathematics only is:
- $\quad 5$
- $\quad 6$
- $\quad 7$
- $\quad 8$
- $\quad 9$
(Source: AHSME 1965)
Circles: GRE Math Practice Question#7
If the radius of a circle is increased by $1$ unit, the ratio of the new circumference to the new diameter is:
- $\quad \pi +2$
- $\quad \dfrac{2\pi+1}{2}$
- $\quad \pi$
- $\quad \dfrac{2\pi-1}{2}$
- $\quad \pi-2$
Sum of consecutive integers: GRE Quantitative Comparison Question#8
This GRE quantitative comparison question tests your understanding of sum of consecutive integers.
$\begin{array}{c c c c c}
& \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & \\
& \textrm{Sum of 100 consecutive integers} & & & & \textrm{Sum of 101 consecutive integers} \\
& \textrm{beginning with 101.} & & & & \textrm{beginning with 100.} \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Distance and rate problem: GRE Math Practice Question#9
This GRE Math practice problem tests your understanding of how to formulate distance and rate problems.
Mr. Earl E. Bird leaves his house for work at exactly $8:00$ A.M. every morning. When he averages $40$ miles per hour, he arrives at his workplace three minutes late. When he averages $60$ miles per hour, he arrives three minutes early. At what average speed, in miles per hour, should Mr. Bird drive to arrive at his workplace precisely on time?
- $\quad 45$
- $\quad 48$
- $\quad 50$
- $\quad 55$
- $\quad 58$
Standard deviation: GRE Quantitative Comparison Question#10
This GRE quantitative comparison question tests your qualitative understanding of standard deviation.
$$
\begin{array}{c}
b-a=10 \\
c-b=4
\end{array}
$$
$\begin{array}{c c c c c c}
& \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & \\
& \textrm{Standard deviation of $a$, $b$, and $c$} & & & & \textrm{Standard deviation of $2$, $12$, and $16$} \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Decimals and Scientific Notation: GRE Quantitative Comparison Question#11
This GRE quantitative comparison question tests your understanding of decimals and scientific notation.
$\begin{array}{c c c c c}
& \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & \\
& 0.000329 & & & & 0.32(10^{-3}) + 90(10^{-6}) \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Sequences with patterns: GRE Math Practice Question#12
This GRE Math practice problem tests your understanding of sequences and identifying patterns.
The first term of a sequence is $2005$. Each succeeding term is the sum of the cubes of the digits of the previous term. What is the $2005^{\textrm{th}}$ term of the sequence?
- $\quad 29$
- $\quad 55$
- $\quad 85$
- $\quad 133$
- $\quad 250$
Right triangles: GRE Quantitative Comparison Question#13
This GRE quantitative comparison question tests your understanding of basic geometric properties of right triangles.
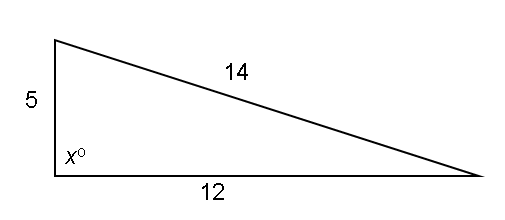
$\begin{array}{c c c c c c}
& \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & \\
& x & & & & 90 \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Square and Equilateral Triangle: GRE Quantitative Comparison Question#14
This GRE quantitative comparison question tests your understanding of basic geometric properties of squares and equilateral triangles.
$\begin{array}{c c c c c c c c c c c}
& & \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & & \\
& & \textrm{The area of a square with a} & & & & \textrm{The area of an equilateral triangle} \\
& & \textrm{diagonal of length 2} & & & & \textrm{with a height of 2} \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Mixtures and fractions: GRE Math Practice Question#15
This GRE Math practice problem tests your understanding of mixtures and fractions.
Two $600$ ml pitchers contain orange juice. One pitcher is $\frac{1}{3}$ full and the other pitcher is $\frac{2}{5}$ full. Water is added to fill each pitcher completely, then both pitchers are poured into one large container. What fraction of the mixture in the large container is orange juice?
- $\quad \dfrac{1}{8}$
- $\quad \dfrac{3}{16}$
- $\quad \dfrac{11}{30}$
- $\quad \dfrac{11}{19}$
- $\quad \dfrac{11}{15}$
(Source: 2004 AMC 8)
Algebraic Word Translations: GRE Quantitative Comparison Question#16
This GRE quantitative comparison question tests your understanding of algebraic word translations.
In a container, the number of red balls is five less than twice the number of blue balls. The container has a total of $40$ balls, and $30$ percent of the balls are neither red nor blue.
$\begin{array}{c c c c c c}
& \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & \\
& \textrm{The number of red balls} & & & & 19 \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Sequences with patterns: GRE Math Practice Question#17
This GRE Math practice problem tests your understanding of sequences and identifying patterns.
Let $a_1, a_2, a_3, \ldots, a_n$ be a sequence of numbers where $a_1=-2$, $a_2=4$, and for $n \geq 3$, $a_n = \left(\dfrac{a_{n-1}}{a_{n-2}}\right)$. What is the sum of the first $99$ terms?
- $\quad -16$
- $\quad -12$
- $\quad -8$
- $\quad -4$
- $\quad 0$
Prime Factorization: GRE Quantitative Comparison Question#18
This GRE quantitative comparison question tests your understanding of prime factorization.
$$ n = (15^3) (25^4) (12^6) (28^3) $$
$\begin{array}{c c c c c}
& \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & \\
& \textrm{The number of distinct prime factors of $n$} & & & & 5 \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Statistics, average (arithmetic mean): GRE Math Practice Question#19
This GRE Math practice problem tests your understanding of averages(arithmetic mean) in statistics.
The average (arithmetic mean) of a list of thirteen numbers is $17$. A new number is added to the list, and the average (arithmetic mean) of this new set of numbers is $18$. What number has been added?
- $\quad 13$
- $\quad 27$
- $\quad 31$
- $\quad 39$
- $\quad \textrm{It cannot be determined based on the information above}$
Algebraic Word Translations: GRE Quantitative Comparison Question#20
This GRE quantitative comparison question tests your understanding of algebraic word translations.
After removing $6$ green balls from a container, there are twice as many red balls as green balls. Then $15$ red balls are removed from the container and there are three times as many green balls as red balls.
$\begin{array}{c c c c c c c c}
& & & \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & & & \\
& & & \textrm{The total number of green and red balls in} & & & & 36 \\
& & & \textrm{the container before removing the 6 green balls.} & & & & \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Geometry(Triangles and Angles): GRE Math Practice Question#21
This GRE Math practice problem tests your understanding of angle relationships in a triangle.
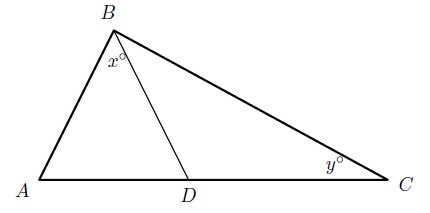
In the figure above, $\overline{AB} \perp \overline{BC}$, and $\overline{AB} = \overline{AD}$. What is $y$ in terms of $x$ ?
- $\quad x-90$
- $\quad 2x-90$
- $\quad 90-x$
- $\quad 90-2x$
- $\quad \dfrac{x}{2}$
Algebra and reciprocals: GRE Math Practice Question#22
This GRE Math practice problem tests your understanding of reciprocals and algebraic rearrangement.
Which of the following equals the reciprocal of $\dfrac{1}{x} \,-\, x$, where $x \neq 1$?
- $\quad x \,- \dfrac{1}{x}$
- $\quad \dfrac{x}{x^2-1}$
- $\quad \dfrac{x}{1-x^2}$
- $\quad \dfrac{x^2-1}{x}$
- $\quad \dfrac{1-x^2}{x}$
Largest factor of an exponent expression: GRE Math Practice Question#23
This GRE Math practice problem tests your understanding of prime factorization.
What is the greatest integer value of $n$ such that $18^{9}$ is divisible by $3^n$ ?
- $\quad 9$
- $\quad 12$
- $\quad 18$
- $\quad 27$
- $\quad 36$
Arithmetic/Percentage Change: GRE Math Practice Question#24
This GRE Math practice problem tests your understanding of percent change and decimals.
$2 \times 10^{-4}$ is what percent greater than $5 \times 10^{-5}$?
- $\quad 4\%$
- $\quad 75\%$
- $\quad 300\%$
- $\quad 900\%$
- $\quad 4000\%$
Geometry (Isosceles Triangles): GRE Quantitative Comparison Question#25
This GRE quantitative comparison question tests your understanding of properties of isosceles triangles.
The lengths of two sides of an isosceles triangle are $3$ and $7$.
$\begin{array}{c c c c c c c c c c c}
& & & & & & \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & & & & & & \\
& & & & & & \textrm{The perimeter of the triangle} & & & & \textrm{17} \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Geometry/Percent Change: GRE Math Practice Question#26
This GRE Math practice problem tests your understanding of percent change in the context of geometric area.
If the diameter of a circle is reduced by $40\%$, by what percent will the area of the circle be reduced?
- $\quad 36$
- $\quad 40$
- $\quad 56$
- $\quad 64$
- $\quad 80$
Arithmetic/Product of Numbers: GRE Math Practice Question#27
This GRE Math practice problem tests your understanding of distributive property of multiplication.
$$ 998 \times 999 \times 1000 \times 1001 \times 1002$$
An increase of $1$ in which of the five numbers above would result in the greatest increase in the product?
- $\quad 998$
- $\quad 999$
- $\quad 1000$
- $\quad 1001$
- $\quad 1002$
Rates, Units, and Variables: GRE Math Practice Question#28
This GRE Math practice problem tests your understanding of how to do unit conversions on algebraic quantities.
Water flows from a pipe at the rate of $3r$ gallons for every $m$ minutes. How much water flows through the pipe in $x$ seconds?
- $\quad 3rxm$
- $\quad \dfrac{3rx}{m}$
- $\quad \dfrac{3rm}{x}$
- $\quad \dfrac{20rx}{m}$
- $\quad \dfrac{rx}{20m}$
Units digit of a square of a number: GRE Math Practice Question#29
This GRE quantitative question requires you to understand how the units digit of integers change when they are squared.
If $n$ is a positive two digit integer, then which of the following CANNOT be the units digit of $n^2$?
- $\quad 3$
- $\quad 7$
- $\quad 8$
- $\quad \textrm{I only}$
- $\quad \textrm{II only}$
- $\quad \textrm{I and II only}$
- $\quad \textrm{II and III only}$
- $\quad \textrm{I, II, and III}$
Area of Rectangles and Algebra: GRE Math Practice Question#30
This GRE Math practice problem tests your understanding of geometry problems that rely on algebraic restatement.
The length of rectangle $R$ is $50\%$ greater than the length of rectangle $S$, and the width of rectangle $R$ is twice the width of rectangle $S$. If the area of rectangle $R$ is $x$, then in terms of $x$, the area of rectangle $S$ is how much less than the area of rectangle $R$?
- $\quad \dfrac{x}{3}$
- $\quad \dfrac{x}{2}$
- $\quad \dfrac{2x}{3}$
- $\quad x$
- $\quad 2x$
Divisibility, Sets, and Venn Diagram: GRE Math Practice Question#31
This GRE Math practice problem tests your understanding of dealing with divisibility, sets, and using Venn diagrams.
Set $A$ consists of all positive integers less than or equal to $100$ that are divisible by $4$. Set $B$ consists of all positive integers less than or equal to $100$ that are divisible by $6$. How many of the integers in Set $A$ are not in Set $B$?
- $\quad 8$
- $\quad 16$
- $\quad 17$
- $\quad 21$
- $\quad 25$
Negative Exponents and Quadratics: GRE Math Practice Question#32
This GRE Math practice problem tests your understanding of dealing with quadratics that are presented in a different form.
If $12 x^{-2} – 5 x^{-1} = 2$, which of the following could be the value of $x$?
- $\quad 4$
- $\quad \dfrac{3}{2}$
- $\quad \dfrac{2}{3}$
- $\quad -\dfrac{2}{3}$
- $\quad -\dfrac{3}{2}$
Multiples and Sets: GRE Math Practice Question#33
This GRE Math practice problem tests your understanding of counting multiples and using set principles to answer the question.
What is the number of integers from $1$ to $1000$ that are divisible by $24$ but not by $15$?
- $\quad 33$
- $\quad 35$
- $\quad 37$
- $\quad 39$
- $\quad 41$
Geometry and Algebra: GRE Quantitative Comparison Question#34
This GRE quantitative comparison question tests your understanding of geometry and putting an algebraic structure to the question.
The perimeter of a square and a rectangle in feet are equal. The length of the rectangle is $1$ foot longer than the width.
$\begin{array}{c c c c c c c c c c c}
& & & & & & \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & & & & & & \\
& & & & & & \textrm{Area of square} & & & & \textrm{Area of rectangle} \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Mixtures and Dilution: GRE Math Practice Question#35
This GRE Math practice problem tests your ability to formulate mixture problems using algebraic relationships.
To $m$ ounces of an $m \%$ solution of acid, $x$ ounces of water are added to yield an $(m-10)\%$ solution. If $m \gt 25$, then $x$ is:
- $\quad \dfrac{10m}{m-10}$
- $\quad \dfrac{5m}{m-10}$
- $\quad \dfrac{m}{m-10}$
- $\quad \dfrac{5m}{m-20}$
- $\quad \textrm{not determined by the given information}$
Ratios and Algebraic Manipulation: GRE Math Practice Question#36
This GRE Math practice problem tests your understanding of ratios and algebraic manipulation.
If $\dfrac{m}{n} = \dfrac{4}{3}$ and $\dfrac{r}{t}= \dfrac{9}{14}$, the value of $\dfrac{3mr-nt}{4nt-7mr}$ is:
- $\quad -5\frac{1}{2}$
- $\quad -\dfrac{11}{14}$
- $\quad -1\frac{1}{4}$
- $\quad \dfrac{11}{14}$
- $\quad -\dfrac{2}{3}$
Right Isosceles Triangle(Area and Perimeter): GRE Math Practice Question#37
This GRE Math practice problem tests your understanding of roots of a quadratic equation.
The perimeter of an isosceles right triangle is $2p$. Its area is:
- $\quad (2+\sqrt{2})p$
- $\quad (2-\sqrt{2})p$
- $\quad (3-2\sqrt{2})p^2$
- $\quad (1-2\sqrt{2})p^2$
- $\quad (3+2\sqrt{2})p^2$
Manipulating Algebraic Expressions: GRE Math Practice Question#38
This GRE quantitative comparison question tests your ability to manipulate algebraic expressions and also apply exponent rules in the process.
$$a=\dfrac{2}{b^2}$$
$\begin{array}{c c c c c c c c c c c}
& & & & & & \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & & & & & & \\
& & & & & & (a^2)^3(b^3)^4 & & & & 64 \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Roots of Quadratic Equations: GRE Practice Question#39
This GRE Math practice problem tests your understanding of roots of a quadratic equation.
The sum of the reciprocals of the roots of the equation $x^2 + px + q=0$ is:
- $\quad -\dfrac{p}{q}$
- $\quad \dfrac{q}{p}$
- $\quad \dfrac{p}{q}$
- $\quad -\dfrac{q}{p}$
- $\quad pq$
Equations with Exponent terms: GRE Practice Question#40
This GRE Math practice problem tests your understanding of exponents and how to manipulate their algebraic forms.
If $9^{x+2} = 240 + 9^{x}$, then the value of $x$ is:
- $\quad 0.1$
- $\quad 0.2$
- $\quad 0.3$
- $\quad 0.4$
- $\quad 0.5$
Word Problem on Algebra and Ratio: GRE Math Practice Question#41
This GRE Math practice problem tests your understanding of ratios, percentages, and the ability to make algebraic translations.
John ordered $4$ pairs of black socks and some additional pairs of blue socks. The price of the black socks per pair was twice that of the blue. When the order was filled, it was found that the number of pairs of the two colors had been interchanged. This increased the bill by $50\%$. The ratio of the number of pairs of black socks to the number of pairs of blue socks in the original order was:
- $\quad 4:1$
- $\quad 2:1$
- $\quad 1:4$
- $\quad 1:2$
- $\quad 1:8$
Prime Factors: GRE Quantitative Comparison Question#42
This GRE quantitative comparison question tests your understanding of prime factorization.
$\begin{array}{c c c c c c}
& \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & \\
& \textrm{The least positive integer with three distinct prime} & & & & 1000 \\
& \textrm{factors, each greater than 5} & & & & \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Exponents: GRE Quantitative Comparison Question#43
This GRE quantitative comparison question tests your ability to manipulate quantities with large powers.
$\begin{array}{c c c c c c c c c c c}
& & & & & & \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & & & & & & \\
& & & & & & \dfrac{6^{36}}{4^{12}} & & & & (9^{17})(4^{8}) \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Algebraic Inequalities: GRE Math Practice Question#44
This problem tests your understanding of the basic properties of inequalities that are tested on the math section of the Revised GRE test. I have included my video explanation for this problem.
Given $x \gt 0$, $y \gt 0$, $x \gt y$, and $z \neq 0$. The inequality which is not always correct is
- $\quad x+z \gt y+z$
- $\quad x – z \gt y – z$
- $\quad xz \gt yz$
- $\quad \dfrac{x}{z^2} \gt \dfrac{y}{z^2}$
- $\quad x z^2 \gt y z^2$
Counting: GRE Math Practice Question#45
This GRE Math practice problem tests your understanding of counting principles and their application.
A total of $28$ handshakes was exchanged at the conclusion of a party. Assuming that each participant shook hands with all the others, the number of people present was
- $\quad 56$
- $\quad 28$
- $\quad 14$
- $\quad 8$
- $\quad 7$
Place Value and Divisibility: GRE Math Practice Question#46
This GRE Math practice problem tests your understanding of the divisibility rules.
A “palindrome” is any integer that reads the same backward and forward. A six-digit positive palindrome must be divisible by which of the following?
- $\quad 3$
- $\quad 7$
- $\quad 9$
- $\quad 11$
- $\quad 13$
Remainders and Quotients: GRE Math Practice Question#47
This GRE Math practice problem tests your understanding of the remainder algorithm and how to express the relationship between divisors, remainders, and quotients.
When $n$ is divided by 6, the remainder is 3, and the quotient is $q$. When $3n+2$ is divided by 6, the remainder is 5, and the quotient in terms of $q$, is
- $\quad \displaystyle \frac{q}{3}$
- $\quad \displaystyle \frac{q}{3}+2$
- $\quad 3q$
- $\quad 3q+1$
- $\quad 3q+2$
Linear Systems of Equations and No Solutions: GRE Math Practice Question#48
This question tests your understanding of the conditions under which a linear system of equations has no solutions, and how it conceptually relates to the graph of linear equations.
ax-3y=-7 \\
-4x+6y=5
\end{eqnarray}$
In the linear system of equations above, what value of $a$ would given no solutions?
- $\quad -2$
- $\quad -4$
- $\quad 1$
- $\quad 2$
- $\quad 4$
Regular hexagon and right triangles: GRE Math Practice Question#49
This question tests your understanding of the relationship between internal angles and sides of a regular hexagon.
Opposite sides of a regular hexagon are $12$ inches apart. The length of each side, in inches, is
- $\quad 7.5$
- $\quad 6\sqrt{2}$
- $\quad 5\sqrt{2}$
- $\quad \dfrac{9\sqrt{3}}{2}$
- $\quad 4\sqrt{3}$
Counting and arrangements: GRE Math Practice Question#50
This question tests your understanding of basic counting principles applied to creating words with letters repeated and added constraints on their arrangements.
How many distinguishable rearrangements of the letters in $\textbf{CONTEST}$ have both the vowels first? (For instance, $\textbf{OETCNST}$ is one such arrangement, but $\textbf{OTETSNC}$ is not.)
- $\quad 60$
- $\quad 120$
- $\quad 240$
- $\quad 720$
- $\quad 2520$
Successive percentage changes: GRE Math Practice Question#51
This question tests your understanding of algebraically being able to formulate problems on successive percentage changes.
The price of an article was increased $p\%$. Later the new price was decreased $p\%$. If the last price was one dollar, the original price was:
- $\quad \dfrac{1-p^2}{200}$
- $\quad \dfrac{\sqrt{1-p^2}}{100}$
- $\quad \textrm{one dollar}$
- $\quad 1- \dfrac{p^2}{10000-p^2}$
- $\quad \dfrac{10000}{10000-p^2}$
Chords, circles, and triangles: GRE Math Practice Question#52
This question tests your understanding of calculating areas of non-standard regions in a circle that involves chords and triangles.
Two equal parallel chords are drawn $8$ inches apart in a circle of radius $8$ inches. The area of that part of the circle that lies between the chords is:
- $\quad 21\frac{1}{3}\pi – 32\sqrt{3}$
- $\quad 32\sqrt{3}+21\frac{1}{3}\pi$
- $\quad 32\sqrt{3}+42\frac{2}{3}\pi$
- $\quad 16\sqrt{3}+42\frac{2}{3}\pi$
- $\quad 42\frac{2}{3}\pi$
Digits, permutations, and sequences: GRE Math Practice Question#53
This question tests your understanding of principles of counting.
Each of the five digits $1, 2, 3, 4$, and $5$ is used once to create distinct $5$ digit numbers. If the numbers are ranked from the least to the greatest, what is the last digit of the $62$nd number?
- $\quad 1$
- $\quad 2$
- $\quad 3$
- $\quad 4$
- $\quad 5$
Subtracting algebraic exponent terms: GRE Math Practice Question#54
This question tests your understanding of manipulating algebraic exponent terms.
If $9^{x} – 9^{x-2} = 240$, then $x\left(x-\dfrac{1}{2}\right)=$
- $\quad 3$
- $\quad 4$
- $\quad 5$
- $\quad 6$
- $\quad 9$
Tough distance/rate/time problem: GRE Math Practice Question#55
This question tests your understanding of algebraic formulation of distance/rate/time problems that are tested on the math section of the revised GRE test.
Two trains, $m$ miles apart, when traveling towards each other on parallel tracks pass each other in $t$ hours. If the same two trains were to travel in the same direction, starting $m$ miles apart, they would meet each other in $u$ hours. What is the ratio of the speed of the faster train to that of the slower train?
- $\quad \dfrac{u}{t}$
- $\quad \dfrac{2u}{u+t}$
- $\quad \dfrac{u+t}{u-t}$
- $\quad \dfrac{u}{u-t}$
- $\quad \dfrac{u+t}{t}$
Multiple machines and work: GRE Math Practice Question#56
This GRE math practice question tests your understanding of how to deal with work problems that involve multiple machines.
An operator can finish a job with a certain number of identical machines in $4$ days. If the operator had $4$ more of these same machines, the job could be completed in $3$ days. If the machines all work at the same rate, how many days would it take one machine to complete the same job?
- $\quad 6$
- $\quad 12$
- $\quad 36$
- $\quad 48$
- $\quad 72$
Manipulating algebraic expressions: GRE Math Practice Question#57
This GRE quantitative comparison question tests your ability to recognize identities and to be able to manipulate algebraic expressions.
$$
\begin{array}{c}
x+y=\dfrac{5}{2} \\
xy=-6
\end{array}
$$
$\begin{array}{c c c c c c c c c c c}
& & & & & & \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & & & & & & \\
& & & & & & x^2+y^2-xy & & & & 25\\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Factors of a large number: GRE Math Practice Question#58
This GRE quantitative question requires you to find factors of large numbers by using basic algebraic identities.
If $n=2^{48}-1$, then $n$ is divisible by which of the following?
- $\quad 5$
- $\quad 7$
- $\quad 13$
- $\quad \textrm{None}$
- $\quad \textrm{I and II only}$
- $\quad \textrm{I and III only}$
- $\quad \textrm{II and III only}$
- $\quad \textrm{I, II, and III}$
Area of a framed painting: GRE Math Practice Question#59
This GRE quantitative question requires you to algebraically represent the lengths and widths in a rectangular pictures frame and translate the given condition to a quadratic equation.
A painting $18” \times 24”$ is to be placed into a wooden frame with the longer dimension vertical. The wood at the top and bottom is twice as wide as the wood on the sides. If the frame area equals that of the painting itself, the ratio of the smaller to the larger dimension of the framed painting is:
- $\quad 1:3$
- $\quad 1:2$
- $\quad 2:3$
- $\quad 3:4$
- $\quad 1:1$
Similar triangles and area: GRE Math Practice Question#60
This GRE quantitative question requires you to identify similar triangles and use this relationship to find the ratio of areas of two triangles.
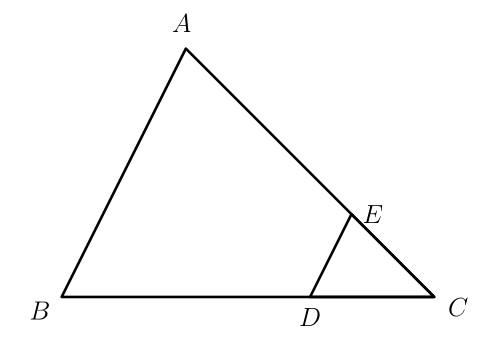
In triangle $ABC$ shown above, $DE$ is parallel to $AB$. If the point $D$ divides the line segment $BC$ such that $BD$ is twice the length of $DC$, then what is the ratio of the area of triangle $ABC$ to triangle $EDC$ ?
- $\quad 3 \; \textrm{to} \; 1$
- $\quad 4 \; \textrm{to} \; 1$
- $\quad 6 \; \textrm{to} \; 1$
- $\quad 8 \; \textrm{to} \; 1$
- $\quad 9 \; \textrm{to} \; 1$
Word problems and algebraic formulation: GRE Math Practice Question#61
Try this GRE question that tests your ability to formulate algebraic equations in the context of a word problem.
Some marbles in a bag are red and the rest are blue. If one red marble is removed, then one-seventh of the remaining marbles are red. If two blue marbles are removed instead of one red, then one-fifth of the remaining marbles are red. How many marbles were in the bag originally?
- $\quad 8 $
- $\quad 22 $
- $\quad 36 $
- $\quad 57 $
- $\quad 71 $
Exponents and manipulations: GRE Math Practice Question#62
Try this GRE question that tests your ability to rewrite exponents terms in commonly used bases and simplify them by factoring terms.
$\sqrt{\dfrac{8^{10}+4^{10}}{8^4+4^{11}}}=$
- $\quad \sqrt{2} $
- $\quad 16 $
- $\quad 32 $
- $\quad 12^{2/3} $
- $\quad 512.5 $
Intersection of a rectangle and a circle: GRE Math Practice#63
Try this geometry question that tests your understanding of rectangles, circles, arcs, and standard right triangles.
An $8$ by $2\sqrt{2}$ rectangle has the same center as a circle of radius $2$. The area of the region common to both the rectangle and the circle is
- $\quad 2\pi $
- $\quad 2\pi + 2 $
- $\quad 4\pi – 4 $
- $\quad 2\pi + 4$
- $\quad 4\pi – 2 $
Statistics and averages: GRE Math Practice Question#64
Try this GRE question that tests your ability to manipulate the equation of average (arithmetic mean) of a large set of numbers.
After finding the average of $35$ scores, a student carelessly included the average with the $35$ scores and found the average of these $36$ numbers. The ratio of the second average to the true average was
- $\quad 1:1 $
- $\quad 35: 36 $
- $\quad 36: 35 $
- $\quad 2: 1 $
- $\quad \textrm{None of the above} $
Similar triangles and area: GRE Math Practice Question#65
Try this GRE question that tests your understanding of finding areas of shaded regions, and also on how the areas of similar triangles are related to the ratios of lengths of the corresponding sides of the two triangles.
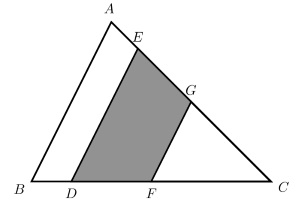
In the triangle $ABC$ shown above the line segments $BA$, $DE$, and $FG$ are parallel to each other. The lengths of segments $BD$, $DF$ and $FC$ are in the ratio of $1$ to $2$ to $3$. What is the ratio of the area of the shaded region to the area of the unshaded region in triangle $ABC$ ?
- $\quad \dfrac{16}{27} $
- $\quad \dfrac{3}{4} $
- $\quad \dfrac{4}{5} $
- $\quad \dfrac{5}{6} $
- $\quad \dfrac{8}{9} $
Triangle area in coordinate plane: GRE Math Practice Question#66
Try this GRE question that tests your understanding of the equation of straight lines and the area of triangle in the $xy$-coordinate plane.
A vertical line divides the triangle with vertices $(0, 0), (1,1)$ and $(9, 1)$ in the $xy-$plane into two regions of equal area. The equation of the line is $x=$
- $\quad 2.5 $
- $\quad 3.0 $
- $\quad 3.5 $
- $\quad 4.0 $
- $\quad 4.5 $
Square inscribed in a circle: GRE Math Practice Question#67
Try this GRE math practice question that tests your understanding of relationship between the length of an edge of a square inscribed in a circle and the radius of the circle.
Question#67: If a square is inscribed in a circle of radius $r$ as shown below, then the area of the shaded region is

- $\quad r^2\left(\pi \; – \, \dfrac{1}{2\pi}\right) $
- $\quad r^2\left(\pi-\dfrac{1}{2}\right) $
- $\quad \dfrac{\pi r^2}{2} $
- $\quad r^2(\pi-1) $
- $\quad r^2(\pi-2) $
Angle in an almost right triangle: GRE Quantitative Comparison Question#68
Try this GRE quantitative comparison question on geometry that tests your understanding of how the right angle of a triangle changes when the dimensions of the legs are changed.
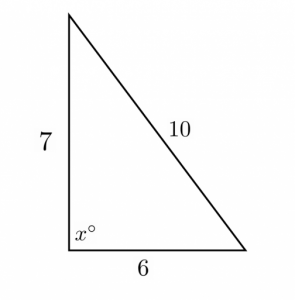
$\begin{array}{c c c c c c c c c c c}
& & & & & & \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & & & & & & \\
& & & & & & x & & & & 90\\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Fractions in word problems: GRE Math Practice Question#69
Try this GRE math practice question that tests your ability to translate word relationships when given in terms of fractions.
Question#69: In the month of June, Ryan used $\dfrac{1}{12}$ of his monthly salary for his student loan payment. Ryan also paid $\dfrac{2}{3}$ more than the student loan payment for his rent. What fraction of his monthly salary was left after Ryan made the student loan and rent payment?
- $\quad \dfrac{31}{36}$
- $\quad \dfrac{7}{9}$
- $\quad \dfrac{5}{8}$
- $\quad \dfrac{3}{4}$
- $\quad \dfrac{1}{4}$
Fractions and patterns: GRE Math Practice Question#70
Try this GRE math practice question that tests your ability to express the problem in terms of fractions and then recognize a pattern.
Question#70: One half of the water is poured out of a full container. Then one third of the remainder is poured out. Continue the process: one fourth of the remainder for the third pouring, one fifth of the remainder for the fourth pouring, etc. After how many pourings does exactly one tenth of the original water remain?
- $\quad 6$
- $\quad 7$
- $\quad 8$
- $\quad 9$
- $\quad 10$
Algebraic fractions and manipulation : GRE Math Practice Question#71
Try this GRE math practice question that tests your ability to manipulate and rearrange algebraic expressions to isolate one variable in terms of another variable.
Question#71: If $y = \dfrac{m}{m-n}$ and $x = \dfrac{n}{m+n}$, what is $y$ in terms of $x$?
- $\quad \dfrac{1-x}{1-2x}$
- $\quad \dfrac{1-x}{2x-1}$
- $\quad \dfrac{x}{1-x}$
- $\quad \dfrac{x}{x-1}$
- $\quad \dfrac{1-x}{x}$
Right triangles, area, and percent changes : GRE Math Practice Question#72
GRE Math Practice: This GRE quantitative comparison question tests your understanding of percent changes and area of right triangles.
Question#72: In right triangle $ABC$, the length of the height is increased by $25\%$ and the length of the base is decreased by $25\%$ to create a new right triangle $DEF$.
$\begin{array}{c c c c c c}
& \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & \\
& \textrm{Area of triangle $ABC$} & & & & \textrm{Area of triangle $DEF$}\\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Simplifying algebraic fractions: GRE Math Practice Question#73
Try this GRE math practice question that tests your ability to simplify algebraic fractions.
Question#73: If $x > 0$, $y > 0$, and $xy \neq 1$, $\quad$ $x \ – \ \dfrac{1}{\dfrac{1}{x}-y}=$
- $\quad \dfrac{xy}{1-xy}$
- $\quad \dfrac{x^2 y}{xy-1}$
- $\quad \dfrac{x^2 – xy – 1}{x}$
- $\quad \dfrac{x-x^2y-1}{1-xy}$
- $\quad \dfrac{x^2 y – 2x}{xy-1}$
Video explanation
Comparing decimals represented in exponent form: GRE Math Practice Question#74
Try this GRE math practice question that tests your ability to manipulate and compare decimals expressed in exponent form.
Question#74:
Comparing the numbers $10^{-49}$ and $2 \cdot 10^{-50}$ we may say:
-
$\quad \textrm{the first exceeds the second by $8 \cdot 10^{-1}$}$
-
$\quad \textrm{the first exceeds the second by $2 \cdot 10^{-1}$}$
-
$\quad \textrm{the first exceeds the second by $8 \cdot 10^{-50}$}$
-
$\quad \textrm{the second is five times the first}$
-
$\quad \textrm{the first exceeds the second by 5}$
Video explanation
Circle and inscribed square: GRE Math Practice Question#75
Try this GRE math practice question that tests your understanding of the link between the radius of a circle and the length of the side of an inscribed square.
Question#75:
The circumference of a circle is $10$ inches. The area of a square inscribed in this circle, expressed in square inches, is:
-
$\quad \displaystyle \frac{25}{2\pi^2}$
-
$\quad \displaystyle \frac{50}{\pi^2}$
-
$\quad \displaystyle \frac{100}{\pi^2}$
-
$\quad \displaystyle \frac{200}{\pi^2}$
-
$\quad 50$
Video explanation
Exponents and division: GRE Math Practice Question#76
Try this GRE math practice question that tests your understanding of how to manipulate and simplify exponents. This is also a good example of a question where the on-screen calculator provided on the GRE test is of no use.
Question#76:
$\displaystyle \frac{15^{30}}{45^{15}}=$
-
$\quad \displaystyle \left(\frac{1}{3}\right)^{15}$
-
$\quad \displaystyle \left(\frac{1}{3}\right)^{2}$
-
$\quad 1$
-
$\quad 3^{15}$
-
$\quad 5^{15}$
Video explanation
Square inscribed in a square: GRE quantitative reasoning question #77
Try the following GRE quantitative reasoning question that tests your understanding of inscribed squares and application of Pythagorean theorem to find distances.
Question#77:
A square of perimeter $20$ is inscribed in a square of perimeter $28$. What is the greatest distance between a vertex of the inner square and a vertex of the outer square?
-
$\quad \sqrt{58}$
-
$\quad \displaystyle \frac{7\sqrt{5}}{2}$
-
$\quad 8$
-
$\quad \sqrt{65}$
-
$\quad 5\sqrt{3}$
Video explanation
Coins, values, and system of equations: GRE quantitative reasoning question #78
Try the following GRE quantitative reasoning question that tests your ability to translate word problems to an algebraic system of equations.
Question#78:
Joe has a collection of $23$ coins, consisting of $5$-cent coins, $10$-cent coins, and $25$-cent coins. He has $3$ more $10$-cent coins than $5$-cent coins, and the total value of his collection is $320$ cents. How many more $25$-cent coins does Joe have than $5$-cent coins?
-
$\quad 0$
-
$\quad 1$
-
$\quad 2$
-
$\quad 3$
-
$\quad 4$
Word problem on percentages: GRE quantitative reasoning question #79
Try the following GRE quantitative reasoning question that tests your ability to translate word problems on percentages and solve them algebraically.
Question#79:
Some boys and girls are having a car wash to raise money for a class trip to China. Initially $40\%$ of the group are girls. Shortly thereafter two girls leave and two boys arrive, and then $30\%$ of the group are girls. How many girls were initially in the group?
-
$\quad 4$
-
$\quad 6$
-
$\quad 8$
-
$\quad 10$
-
$\quad 12$
Largest prime factor : GRE Math Practice Question#80
GRE Math Practice: This GRE quantitative comparison question tests your understanding of prime factors and algebraic identities.
Question#80:
$\begin{array}{c c c c c c c}
& \underline{\textrm{Quantity A}} & & & & & \underline{\textrm{Quantity B}} \\
& & & & & &\\
& \textrm{The greatest prime factor of} & & & & & \textrm{$30$}\\
& \textrm{$(2^{5})^2-1$} & & & & & \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Average rate problems: GRE quantitative reasoning question #81
Try the following GRE quantitative reasoning question on average rate problems that are commonly tested on the GRE.
Question#81:
A man travels $m$ feet due north at $\textit{$2$ minutes per mile}$. He returns due south to his starting point at $\textit{$2$ miles per minute}$. The average rate in miles per hour for the entire trip is:
-
$\quad 75$
-
$\quad 48$
-
$\quad 45$
-
$\quad 24$
-
$\quad \textrm{impossible to determine without knowing the value of $m$}$
Machines and work problems: GRE quantitative reasoning question#82
Try the following numeric entry GRE quantitative reasoning question that tests your understanding of how to approach multiple machines and work problems.
Numeric Entry Question#82:
If $5$ Type-$A$ pumps working independently can fill a combined total of $5$ identical Size-$B$ tanks in $5$ hours, then $50$ Type-$A$ pumps working independently can fill a combined total of $50$ Size-$B$ tanks in how many hours?
Defined operations: GRE quantitative reasoning question #83
Try the following GRE quantitative reasoning question on defined operations that are tested on the GRE test.
Question#83:
If the operation $x \star y$ is defined by $x \star y = (x+1)(y+1) – 1$, then which one of the following is $\textbf{false}$?
-
$\quad x \star y = y\star x \text{ for all real } x \; \text{and} \; y.$
-
$\quad x \star (y + z) = ( x \star y ) + (x \star z) \text{ for all real } x,y, \text{ and } z.$
-
$\quad (x-1) \star (x+1) = (x \star x) – 1 \text{ for all real } x.$
-
$\quad x \star 0 = x \text{ for all real } x.$
-
$\quad x \star (y \star z) = (x \star y) \star z \text{ for all real } x,y, \text{ and } z.$
Finding a pattern: GRE quantitative reasoning question #84
Try the following GRE quantitative reasoning question that tests your ability to recognize a pattern.
Question#84:
Wanda, Darren, Beatrice, and Chi are tutors in the school math lab. Their schedule is as follows: Darren works every third school day, Wanda works every fourth school day, Beatrice works every sixth school day, and Chi works every seventh school day. Today they are all working in the math lab. In how many school days from today will they next be together tutoring in the lab?
-
$\quad 42$
-
$\quad 84$
-
$\quad 126$
-
$\quad 178$
-
$\quad 252$
Sum of roots: GRE quantitative reasoning question#85
Try the following numeric entry GRE quantitative reasoning question that tests your understanding of how find the sum of roots of an equation.
Numeric Entry Question#85:
What is the sum of all the roots of the equation below?
$$(2x+3)(x-4) + (2x+3)(x-6)=0$$
Comparing Algebraic Expressions: GRE Math Practice Question#86
This GRE math practice question on quantitative comparisons tests your ability to manipulate and compare algebraic expressions.
$$x \gt y \gt 0$$
$\begin{array}{c c c c c c c c c c c}
& & & & & & \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & & & & & & \\
& & & & & & \dfrac{x+1}{x} & & & & \dfrac{y+1}{y} \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Arithmetic mean (average): GRE quantitative reasoning question #87
Try the following GRE quantitative reasoning question that tests your understanding of arithmetic mean(average).
Question#87:
The quiz scores of a class with $k > 12$ students have a mean of $8$. The mean of a collection of $12$ of these quiz scores is $14$. What is the mean of the remaining quiz scores in terms of $k$?
-
$\quad \displaystyle \frac{14-8}{k-12}$
-
$\quad \displaystyle \frac{8k-168}{k-12}$
-
$\quad \displaystyle \frac{14}{12} – \frac{8}{k}$
-
$\quad \displaystyle \frac{14(k-12)}{k^2}$
-
$\quad \displaystyle \frac{14(k-12)}{8k}$
Prime factorization and perfect cubes: GRE quantitative reasoning question #88
Try the following GRE quantitative reasoning question that tests your understanding of prime factorization and how it applies to forming perfect cubes.
Question#88:
Suppose that $m$ and $n$ are positive integers such that $75m = n^{3}$. What is the minimum possible value of $m + n$?
-
$\quad 15$
-
$\quad 30$
-
$\quad 50$
-
$\quad 60$
-
$\quad 5700$
Exponent manipulation: GRE quantitative reasoning question #89
Try the following GRE quantitative reasoning question that tests your ability to manipulate exponent expressions.
Question#88:
Let $n=8^{2022}$. Which of the following is equal to $\displaystyle \frac{n}{4}?$
-
$\quad 4^{1010}$
-
$\quad 2^{2022}$
-
$\quad 8^{2018}$
-
$\quad 4^{3031}$
-
$\quad 4^{3032}$
Comparing and Manipulating Algebraic Expressions: GRE Math Practice Question#90
This GRE math practice question on quantitative comparisons tests your ability to manipulate and compare algebraic expressions. See if you can find the fastest way to answer this question.
$$\dfrac{3x-2}{3} \; – \; \dfrac{(2x-1)}{6} = \dfrac{2x-1}{3} \; – \; \dfrac{(3x-2)}{6}$$
$\begin{array}{c c c c c c c c c c c}
& & & & & & \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & & & & & & \\
& & & & & & 3x-2 & & & & 2x-1 \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Hexagons and lengths: GRE quantitative reasoning question #91
Try the following GRE quantitative reasoning question that tests your understanding of regular hexagons and familiar triangles.
Question#91:
A park is in the shape of a regular hexagon $2$ km on a side. Starting at a corner, Alice walks along the perimeter of the park for a distance of $5$ km. How many kilometers is she from her starting point?
-
$\quad \sqrt{13}$
-
$\quad \sqrt{14}$
-
$\quad \sqrt{15}$
-
$\quad \sqrt{16}$
-
$\quad \sqrt{17}$
Mixtures and dilution: GRE quantitative reasoning question #92
Try the following GRE quantitative reasoning question that tests your understanding of how to set up mixtures and dilution questions.
Question#92:
The number of ounces of water needed to reduce $9$ ounces of shaving lotion containing $50\%$ alcohol to a lotion containing $30\%$ alcohol is:
-
$\quad 3$
-
$\quad 4$
-
$\quad 5$
-
$\quad 6$
-
$\quad 7$
Divisors of prime products: GRE Quantitative Comparison Question#93
This GRE quantitative comparison question tests your understanding of finding factors of products of prime numbers.
Question#93:
$\begin{array}{c c c c c}
& \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & \\
& \textrm{The number of positive} & & & & \textrm{The number of positive} \\
& \textrm{integer divisors of $pq$} & & & & \textrm{integer divisors of $p^3$} \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Remainders: GRE quantitative reasoning question #94
Try the following GRE quantitative reasoning question that tests your understanding of remainders.
Question#94:
A box contains gold coins. If the coins are equally divided among six people, four coins are left over. If the coins are equally divided among five people, three coins are left over. If the box holds the smallest number of coins that meets these two conditions, how many coins are left when equally divided among seven people?:
-
$\quad 0$
-
$\quad 1$
-
$\quad 2$
-
$\quad 3$
-
$\quad 5$
Weighted Average: GRE quantitative reasoning question #95
Try the following GRE quantitative reasoning question that tests your understanding of weighted average.
Question#95:
A speaker talked for sixty minutes to a full auditorium. Twenty percent of the audience heard the entire talk and ten percent slept through the entire talk. Half of the remainder heard one third of the talk and the other half heard two thirds of the talk. What was the average number of minutes of the talk heard by members of the audience?
-
$\quad 24$
-
$\quad 27$
-
$\quad 30$
-
$\quad 33$
-
$\quad 36$
Circles and diameter: GRE quantitative reasoning question #96
Try the following GRE quantitative reasoning question that tests your understanding of the relationship between the diameter and area of a circular region.
Question#96:
$$ d = k \sqrt{\dfrac{A}{\pi}} $$
The formula above gives the diameter $d$ of a circular region in terms of its area $A$, then $k=$
-
$\quad 4$
-
$\quad 2$
-
$\quad 1$
-
$\quad \dfrac{1}{2}$
-
$\quad \dfrac{1}{4}$
Squares and integers: GRE Quantitative Comparison Question#97
This GRE quantitative comparison question tests your understanding of integers and their squares.
Question#97:
$\begin{array}{c c c c c}
& \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & \\
& \textrm{The greatest possible value of $n$} & & & & \textrm{$7$} \\
& \textrm{minus the least possible value of $n$} & & & & \textrm{} \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Average (arithmetic mean): GRE quantitative reasoning question #98
Try the following GRE quantitative reasoning question that tests your understanding of the averages (arithmetic mean).
Question#98:
The Dunbar family consists of a mother, a father, and some children. The average age of the members of the family is $20$, the father is $48$ years old, and the average age of the mother and children is $16$. How many children are in the family?
-
$\quad 2$
-
$\quad 3$
-
$\quad 4$
-
$\quad 5$
-
$\quad 6$
Circle and triangles: GRE quantitative reasoning question #99
Try the following GRE quantitative reasoning question that tests your understanding of circles and area of inscribed triangles.
Question#99:
Point $C$ lies on a circle that has center $O$ with a radius of $2$ units. If $\overline{AB}$ is a diameter of the circle, what is the greatest possible area of triangle $ACB$ ?
-
$\quad 2$
-
$\quad 2\sqrt{2}$
-
$\quad 3$
-
$\quad 4$
-
$\quad 4\sqrt{2}$
Algebraic translation: GRE quantitative reasoning question #100
Try the following GRE quantitative reasoning question that tests your ability to translate word statements to an algebraic relationship.
Question#100:
A phone call between two cities costs $\$0.75$ for the first $4$ minutes and $\$0.25$ for each additional minute. If $t$ is an integer greater than $4$, a phone call $t$ minutes long will cost how many $\textbf{dollars}$?
-
$\quad \displaystyle \frac{3t}{4}$
-
$\quad \displaystyle \frac{t-1}{4}$
-
$\quad \displaystyle \frac{t+1}{4}$
-
$\quad \displaystyle \frac{t-3}{2}$
-
$\quad \displaystyle \frac{t+3}{4}$
Distance/rate/time: GRE quantitative reasoning question #101
Try the following GRE quantitative reasoning question that tests your understanding of word problems based on distance, rate, and time relationship.
Question#101:
How many hours does it take a train traveling at an average rate of $40$ mph between stops to travel $a$ miles if it makes $n$ stops of $m$ minutes each?
-
$\quad \displaystyle \frac{3a+2mn}{120}$
-
$\quad \displaystyle 3a+2mn$
-
$\quad \displaystyle \frac{3a+2mn}{12}$
-
$\quad \displaystyle \frac{a+mn}{40}$
-
$\quad \displaystyle \frac{a+40mn}{40}$
Circles and inscribed triangles: GRE quantitative reasoning question #102
Try the following GRE quantitative reasoning question that tests your understanding of geometric relationship between circles and inscribed triangles.
Question#102:
If $p$ is the perimeter of an equilateral triangle inscribed in a circle, the area of the circle is:
-
$\quad \displaystyle \frac{\pi p^2}{3}$
-
$\quad \displaystyle \frac{\pi p^2}{9}$
-
$\quad \displaystyle \frac{\pi p^2}{27}$
-
$\quad \displaystyle \frac{\pi p^2}{81}$
-
$\quad \displaystyle \frac{\pi p^2 \sqrt{3}}{27}$
Decimals and reciprocals: GRE quantitative reasoning question #103
Try the following GRE quantitative reasoning question that tests your understanding of dealing with decimal numbers and fractions.
Question#103:
When the decimal point of a certain positive decimal number is moved four places to the right, the new number is four times the reciprocal of the original number. What is the original number?
-
$\quad 0.0002$
-
$\quad 0.002$
-
$\quad 0.02$
-
$\quad 0.2$
-
$\quad 2$
Arithmetic sequences and median: GRE quantitative reasoning question #104
Try the following GRE quantitative reasoning question that tests your understanding of dealing with questions based on arithmetic sequences and median.
Question#104:
Thirty-one books are arranged from left to right in order of increasing prices. The price of each book differs by $\$2$ from that of each adjacent book. For the price of the book at the extreme right a customer can buy the middle book and the adjacent one. Then:
-
$\quad \textrm{The adjacent book referred to is at the left of the middle book.}$
-
$\quad \textrm{The middle book sells for $\$36$.}$
-
$\quad \textrm{The cheapest book sells for $\$4$.}$
-
$\quad \textrm{The most expensive book sells for $\$64$.}$
-
$\quad \textrm{None of these is correct.}$
Comparing algebraic expressions: GRE Quantitative Comparison Question#105
This GRE quantitative comparison question tests your ability to compare and manipulate algebraic expressions with multiple variables.
Question#105:
$$c-b=b-a=d-c=f-e$$
$\begin{array}{c c c c c}
& \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & \\
& c-a & & & & (f-e)+(c-b) \\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Counting line segments: GRE quantitative reasoning question #106
Try the following GRE quantitative reasoning question that tests your understanding of counting principles that are commonly tested on the GRE.
Question#106:
How many line segments have both their endpoints located at the vertices of a given cube?
-
$\quad 12$
-
$\quad 15$
-
$\quad 24$
-
$\quad 28$
-
$\quad 56$
Distance, rate, and head start: GRE quantitative reasoning question #107
Try the following GRE quantitative reasoning question that tests your understanding of how to deal with distance-rate problems where one person needs to catch up with another person going at a slower rate.
Question#107:
Sunny runs at a steady rate, and Moonbeam runs $m$ times as fast, where $m$ is a number greater than $1$. If Moonbeam gives Sunny a head start of $h$ meters, how many meters must Moonbeam run to overtake Sunny?
-
$\quad hm$
-
$\quad \displaystyle \frac{h}{h+m}$
-
$\quad \displaystyle \frac{h}{m-1}$
-
$\quad \displaystyle \frac{hm}{m-1}$
-
$\quad \displaystyle \frac{h+m}{m-1}$
Triangles and sides: GRE Quantitative Comparison Question#108
Try this GRE quantitative comparison question on comparing lengths of right triangles in plane geometry.

In the figure above $AC > AB$.
$\begin{array}{c c c c c c c c c c c}
& & & & & & \underline{\textrm{Quantity A}} & & & & \underline{\textrm{Quantity B}} \\
& & & & & & & & & & \\
& & & & & & BD & & & & CE\\
\end{array}$
- $\quad \textrm{Quantity A is greater.}$
- $\quad \textrm{Quantity B is greater.}$
- $\quad \textrm{The two quantities are equal.}$
- $\quad \textrm{The relationship cannot be determined from the information given.}$
Place values and perfect squares: GRE quantitative reasoning question #109
Try the following GRE quantitative reasoning question that tests your understanding of how to deal with place value representation of integers and perfect squares.
Question#109:
How many two-digit positive integers $N$ have the property that the sum of $N$ and the number obtained by reversing the order of the digits of $N$ is a perfect square?
-
$\quad 4$
-
$\quad 5$
-
$\quad 6$
-
$\quad 7$
-
$\quad 8$
Hey what’s the origin of these questions–Is this a mixed bunch or from a single source?
Thank for all you do!